|
Tools - Math 'Convincing and Proving' Critiquing 'Proofs' Tasks, Set #4
Always, Sometimes or Never True: Set #1 (solutions) || Set #2 (solutions)
Critiquing 'Proofs': Set #3 (solutions) || Set #4 (solutions)
Malcolm Swan
Mathematics Education
University of Nottingham
Malcolm.Swan@nottingham.ac.uk
Jim Ridgway
School of Education
University of Durham
Jim.Ridgway@durham.ac.uk
The aim of this assessment is to provide the opportunity for you to:
- evaluate 'proofs' of given statements and identify which are correct;
- identify errors in 'proofs'.
1. The Pythagorean' Theorem
Here are three attempts to prove the Pythagorean theorem.
When you add add three consecutive numbers, your answer is always a multiple of three.
Look carefully at each attempt. Which is the best 'proof'? Explain your reasoning as fully as possible.
 Attempt 1:
Attempt 1:
Suppose a right-angled triangle has sides of length a, b and c
Draw squares on the three sides as shown.
Divide these squares into smaller squares.
You can see that the number of squares on the two shorter sides add up to make the number of squares on the longest side.
So: a2 + b2 = c2
|
|
Attempt 2:
|
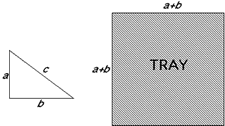
Suppose that you start with four right angled triangles with sides of length a, b and c and a square tray with sides of length a + b.
|
|
|
You can arrange the triangles into the tray in two different ways as shown here.
In the first way, you leave two square holes. These have a combined area of a2 + b2.
In the second way you leave one large square hole. This has an area of c2.
Since these areas are equal
a2 + b2 = c2
|
|
|
|
Attempt 3:
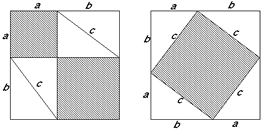
 The proof of the Pythagorean theorem is clear from this diagram.
The proof of the Pythagorean theorem is clear from this diagram.
The squares on the two shorter sides of the black triangle are each made from two congruent triangles.
These fit together to make the square on the longest side- the hypotenuse.
|
The best proof is attempt number ..........
This is because .......
My criticisms of the others are...........
2. Means
Here are two attempts to prove the following result about the arithmetic mean and geometric mean of two numbers:
For any positive numbers a and b,
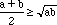
Look carefully at each attempt. Which is the best 'proof'? Explain your reasoning as fully as possible.
|
Attempt 1:
Assuming that
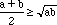
Multiply both sides by 2
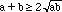
Squaring
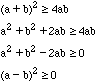
Which is true for positive numbers.
So the assumption was true.
|
Attempt 2:
For all positive numbers
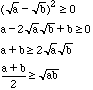
So the result is true.
|
|
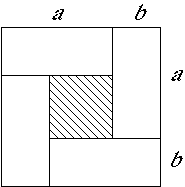
Attempt 3:
Look at the diagram.
The area of the large square =
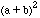 (1) (1)
The unshaded area = 4ab (2)
Since (1) is greater than (2)

So the result is true
|
|
|
The best proof is attempt number ..........
This is because .......
My criticisms of the others are...........
3. Even and Odd
Here are three attempts to prove the following result for natural numbers.
If n2 is an odd number, then n is an odd number.
Look carefully at each attempt. Which is the best 'proof'? Explain your reasoning as fully as possible.
|
Attempt 1:
If n was an even number, then n=2m for some m.
Then n2 = 4m2 = 2(2m2) will also be an even number.
So as n2 is an odd number, then n must be an odd number.
|
|
Attempt 2:
If n was an odd number, then since odd x odd = odd, n2 is also odd.
Then n2 + n would be the sum of two odd integers and would therefore be even.
Since n2 + n = n(n + 1) it is also the product of two consecutive numbers and so it certainly is even. Therefore n is odd.
|
|
Attempt 3:
Since n2 is odd, we have n2 = 4m2 + 4m + 1 for some m.
This means n2= (2m + 1)2 for some m
so n = 2m + 1 which is odd.
|
The best proof is attempt number ..........
This is because .......
My criticisms of the others are...........
Always, Sometimes or Never True: Set #1 (solutions) || Set #2 (solutions)
Critiquing 'Proofs': Set #3 (solutions) || Set #4 (solutions)

|
