Malcolm Swan
Mathematics Education
University of Nottingham
Malcolm.Swan@nottingham.ac.uk

Jim Ridgway
School of Education
University of Durham
Jim.Ridgway@durham.ac.uk

1. Clothing Combinations He was wearing a plaid jacket, porkpie hat, carried a raincoat and wore a camera around his neck, like an ordinary American tourist. As with all Watchers, the hat, jacket and raincoat were soft and reversible, providing six combinations. (The Fourth protocol, Frederick Forsyth)

The article assumes that the hat, jacket and raincoat may each be worn in two ways.

Why does this not give six combinations?

Show how the error should be corrected.

Solution:
The article assumes that the hat, jacket and raincoat may each be worn in two ways.

Here, the error has been to add rather than multiply the possible combinations. If we label the two ways each of the hat, jacket and raincoat may be worn as H1, H2, J1, J2, R1 and R2; then the following diagram shows the eight possible combinations.

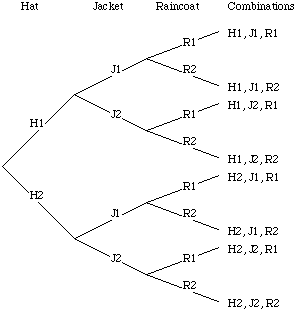
2. Hurley's Syndrome Doctors said that there was a one in four chance that the new baby would inherit Hurley's syndrome. Then it was discovered she was carrying twins and the odds for the disease appearing became one in two. (Sunday Times 5 November 1978)

Explain why the odds for the disease appearing in at least one baby are not one in two.

What is the probability of the disease appearing in at least one of the babies?

Solution:
Again, probablilities have been added inappropriately.

Assuming that probabilities of the two babies having the syndrome are independent, we can list the outcomes in the following tree diagram: (H represents Hurley's syndrome appearing, ~H represents it not appearing).

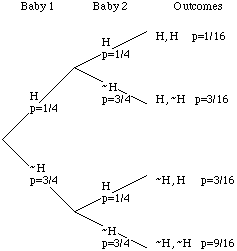
Thus we can see that the probability of the syndrome appearing in at least one baby is ¹/₁₆ + ³/₁₆ + ³/₁₆ = ⁷/₁₆, or just under one half.

3. Double Coin Toss I'll toss two coins. If they both come up heads then Jane wins. If they both come up tails then Ben wins. If we get one head and one tail then I win.

Explain why this is not a fair game.

Solution:
There are four (not three) equally likely outcomes; HH, HT, TH, TT.

Thus I am twice as likely to win as Jane or Ben.

4. Card Sharp A card sharp places three cards into a hat. One card is white on both sides. One card is red on both sides. The remaining card has one white side and one red side. He mixes the cards and asks you to choose one without looking. He places this card on the table. The face now showing is red. The card sharp now says, "It is obvious that this is not the card which is white on both sides. So it must be one of the other two. So the hidden side must be white or red with equal probability. I'll bet you $10 it is red."

Explain why this is not a fair bet.

Solution:
There are not two equally likely cases as it first appears, but three. In one case the other side is white. In both of the other cases it is red, since either side of the red-red card might be showing. The bet, far from being fair is loaded two-to-one in the card sharp's favor.