Malcolm Swan
Mathematics Education
University of Nottingham
Malcolm.Swan@nottingham.ac.uk

Jim Ridgway
School of Education
University of Durham
Jim.Ridgway@durham.ac.uk

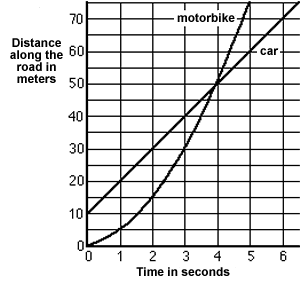
1. Along a country road This graph shows a car and a motorbike travelling along a country road. What is wrong with the following statement? I think that they are travelling at the same speed after 4 seconds. You can tell that because the graphs cross.

Solution:
I think that they are travelling at the same speed after 4 seconds.

You can tell that because the graphs cross.

This statement is false because they are only the same distance along the road at this time. They are travelling at the same speed when the two gradients are the same. This occurs after approx 1.5 seconds. This confusion of position and gradient is a common one among students.

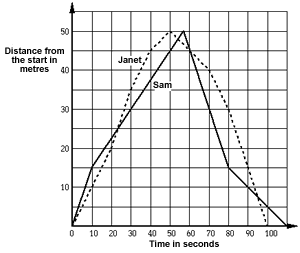
2. Swimming pool The graph above shows the progress of a swimming race. Here is a commentary of the race. Highlight the mistakes in this commentary and write a better one. Sam goes quickly into the lead. He is swimming at 15 metres per second. Janet is swimming at only 10 metres per second. After 22 seconds, Janet overtakes Sam. Janet swims more quickly than Sam from 25 seconds until she turns at 50 seconds. Sam overtakes Janet after 55 seconds, but she catches up again. 5 seconds later, Janet is in the lead until right near the end. Sam swims at a steady 30 metres per second after the turn, until 80 seconds, while Janet is gradually slowing down. Sam wins by 10 seconds.

Explain clearly how you know that an error has been made.

Show how the error should be put right.

Solution:
The faults are italicized and corrected below as bold typeface:

He is swimming at 15 metres per second.
Janet is swimming at only 10 metres per second.
Sam swims at 1.5 meters per second at the start.
Janet swims at 1 meter per second.

Janet swims more quickly than Sam from 25 seconds until she turns at 50 seconds.
Janet swims more quickly than Sam from 10 seconds until 40 seconds after the start.

Sam overtakes Janet after 55 seconds, but she catches up again.
Sam does not overtake Janet after 55 seconds, as they are swimming in opposite directions. He overtakes her after 60 seconds. She does not catch him up until 95 seconds after the start.

5 seconds later, Janet is in the lead until right near the end.
Janet is behind Sam from 60 seconds until 95 seconds.

Sam swims at a steady 30 metres per second after the turn,
Sam swims at 1.5 meters per second after the turn.

until 80 seconds, while Janet is gradually slowing down.
Near the end Janet speeds up.

Sam wins by 10 seconds.
Janet wins by 10 seconds.

A better race commentary would compare positions of swimmers and describe changes in speeds as time evolves. The current description lacks the flavor of a race commentary.

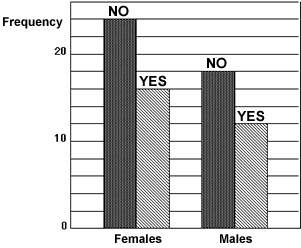
3. College magazine Karl is thinking of producing a college magazine. He produces a prototype of the magazine and conducts a small survey to compare male and female opinions of it. He asks the following question among a random sample of students: Would you pay a dollar for this magazine? The results are shown below.

He concludes that females are less likely to buy the magazine than males.

Explain why Karl is wrong and say what a sensible conclusion would be.

Solution:
Although more females than males say they would not buy the college magazine, this is because his sample contained more females than males. In fact, the proportions of no:yes answers is exactly the same in both groups 24:16 = 18:12 = 3:2. His conclusion should be that there is no difference between male and female views.

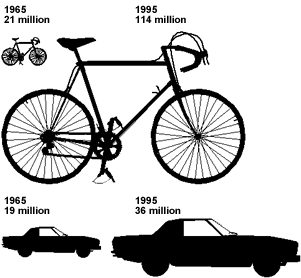
4. Car and Bicycle Production The diagram below shows how the world production of cars and bicycles has changed from 1965 to 1995.

Explain, with reasons, whether or not you think that this diagram fairly represents the numerical information given

Solution:
There were 5.4 times as many bicycles made in 1995 as there were in 1965.

There were 1.9 times as many cars made in 1995 as there were in 1965.

These are correctly reflected in the linear scale factors that have been chosen.

The diagrams, however, are perhaps misleading because they have been enlarged in two dimensions, both the length and height have been multiplied by the scale factor. This gives a superficial impression that the bicycle sales may have grown by about (5.4)² times!