Malcolm Swan
Mathematics Education
University of Nottingham
Malcolm.Swan@nottingham.ac.uk

Jim Ridgway
School of Education
University of Durham
Jim.Ridgway@durham.ac.uk

Over recent years, a number of geographers have tried to find ways of defining the shape of an area. In particular, they have tried to devise a measure of 'compactness'. You probably have some intuitive idea of what "compact" means already. Below are two islands. Island B is more compact than island A. "Compact-ness" has nothing to do with the size of the island. You can have small, compact islands and large compact islands.

Warm-up

Sketch a large 'compact' island and a small 'compact' island.
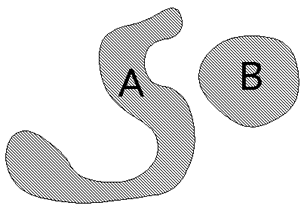
Sketch a large 'less-compact' island and a small 'less-compact' island.

One person has suggested the following way of measuring "compactness."

 

1. Calculate the "compactness" of each of the following 'islands' using the above definition.
   

   
   

   
   

   
   

   
   

2. Use your results to explain why Area ÷ Perimeter is not a suitable definition for "compactness."

   
   

   
   

   
   

   
   

3. Invent your own measure of "compactness".
   Put the shapes A to F in order of "compact-ness" using your measure. Discuss whether or not your measure is better than 'Area ÷ Perimeter.'

   
   

   
   

   
   

   
   

4. Adapt your measure so that it ranges from 0 to 1.
   A perfectly compact shape should have a measure of '1,' while a long, thin, shape should have should have a measure near to 0.

   
   

   
   

   
   

   
   

Square-ness, Example #1 (solution) || Steep-ness, Example #2 (solution)
Compact-ness, Example #3 (solution) || Crowded-ness, Example #4 (solution)
Awkward-ness, Example #5 (solution) || Sharp-ness, Example #6 (solution)