Go to Collaborative Learning Go to FLAG Home Go to Search
Go to Learning Through Technology Go to Site Map
Go to Who We Are
Go to College Level One Home
Go to Introduction Go to Assessment Primer Go to Matching CATs to Goals Go to Classroom Assessment Techniques Go To Tools Go to Resources



Go to Tools overview
Go to Tool search
Go to Tools sorted by discipline
Go to Tools sorted by technique


Tools -Math 'Creating Measures' Compact-ness Task, Example #3 (solution)


Square-ness, Example #1 (solution) || Steep-ness, Example #2 (solution)
Compact-ness, Example #3 (solution) || Crowded-ness, Example #4 (solution)
Awkward-ness, Example #5 (solution) || Sharp-ness, Example #6 (solution)

Malcolm Swan
Mathematics Education
University of Nottingham
Malcolm.Swan@nottingham.ac.uk

Jim Ridgway
School of Education
University of Durham
Jim.Ridgway@durham.ac.uk


This problem gives you the chance to
  • criticise a given measure for the concept of "compact-ness"
  • invent your own way of measuring this concept
  • refine your scale so that it measures from 0 to 1.

Over recent years, a number of geographers have tried to find ways of defining the shape of an area. In particular, they have tried to devise a measure of 'compactness'. You probably have some intuitive idea of what "compact" means already. Below are two islands. Island B is more compact than island A. "Compact-ness" has nothing to do with the size of the island. You can have small, compact islands and large compact islands.

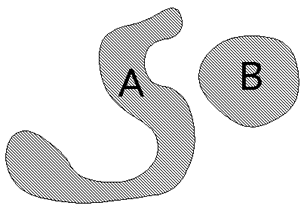
Warm-up

    Sketch a large 'compact' island and a small 'compact' island.
    Sketch a large 'less-compact' island and a small 'less-compact' island.

    One person has suggested the following way of measuring "compactness."

 

Comment:
This question is to make sure that students have followed the introduction. They should all understand that more 'rounded' shapes tend to be compact, while 'long spindly' shapes tend to be less compact.


  1. Calculate the "compactness" of each of the following 'islands' using the above definition.



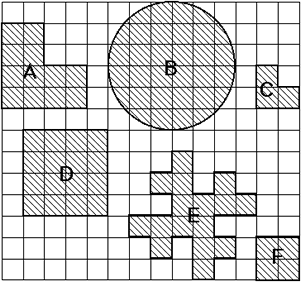
Solution:
The results for area ÷ perimeter for the six shapes are shown below:

Shape
A
B
C
D
E
F
Area
12
28.26
3
16
16
4
Perimeter (cm)
16
18.84
8
16
32
8
Area ÷ Perimeter
0.75
1.5
0.375
1
0.5
0.5







  1. Use your results to explain why Area ÷ Perimeter is not a suitable definition for "compactness."



Solution:
  • While at first the measure area ÷ perimeter might seem reasonable, it is not dimensionless, so it will give different results for enlagements of shapes.

  • Thus in the examples D and F are both squares, but they give different measurements of compactness. Similarly with A and C.







  1. Invent your own measure of "compactness".
    Put the shapes A to F in order of "compact-ness" using your measure. Discuss whether or not your measure is better than 'Area ÷ Perimeter.'



Solution:
A better measure of compactness might therefore be area ÷ (perimeter)2.

This is dimensionless and does give measures in accord with intuition:

Staircase
A
B
C
D
E
F
Area ÷ Perimeter2
0.047
0.080
0.047
0.063
0.016
0.063

Thus, in order of "compactness", we have that

    B (most compact), D and F (tie), A and C (tie), E (least compact).







  1. Adapt your measure so that it ranges from 0 to 1.
    A perfectly compact shape should have a measure of '1,' while a long, thin, shape should have should have a measure near to 0.



Solution:
We could further improve the measure, so that it always lies between 0 and 1 by multiplying by 4. This would make a circle a perfectly compact shape.

The ratio 4A/p2 is quoted in Selkirk (1982) as the "circularity ratio." One criticism of its use by geographers is that it is difficult to define and calculate the perimeter of a very large irregular boundary such as a country or a river basin. (Fractal geometry might suggest that such perimeters may even be infinite!) Instead, there are several other possibilities:

Form Ratio:
A = area
L = length of line joining the area's two most distant points
Compactness ratio:
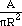A = area
R = radius of the smallest circle which will surround the shape
Radius ratio:
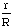r = radius of the largest circle which will fit inside the shape
R = radius of the smallest circle which will surround the shape

These are all quoted in Selkirk (1982) as methods which geographers have used. For interest, Selkirk offers the following calculations for four countries, using these ratios:

Czechoslovakia
Austria
Bulgaria
Romania
Circularity ratio
0.33
0.30
0.43
0.50
Form ratio
0.28
0.30
0.52
0.56
Compactness ratio
0.28
0.30
0.47
0.56
Radius ratio
0.28
0.40
0.46
0.60

Selkirk's results place the countries in a similar order, apart from the circularity ratio, which suggests that Czecholslovakia is less compact than Austria.







Square-ness, Example #1 (solution) || Steep-ness, Example #2 (solution)
Compact-ness, Example #3 (solution) || Crowded-ness, Example #4 (solution)
Awkward-ness, Example #5 (solution) || Sharp-ness, Example #6 (solution)


Got to the top of the page.


Introduction || Assessment Primer || Matching Goals to CATs || CATs || Tools || Resources

Search || Who We Are || Site Map || Meet the CL-1 Team || WebMaster || Copyright || Download
College Level One (CL-1) Home || Collaborative Learning || FLAG || Learning Through Technology || NISE