
|
Tools - Math 'Creating Measures' Sharp-ness Task, Example #6
Square-ness, Example #1 (solution) || Steep-ness, Example #2 (solution)
Compact-ness, Example #3 (solution) || Crowded-ness, Example #4 (solution)
Awkward-ness, Example #5 (solution) || Sharp-ness, Example #6 (solution)
Malcolm Swan
Mathematics Education
University of Nottingham
Malcolm.Swan@nottingham.ac.uk
Jim Ridgway
School of Education
University of Durham
Jim.Ridgway@durham.ac.uk
This task gives you the chance to:
- invent your own measure for the concept of 'difficulty' of going round a bend
- use your measure to put bends in order of 'difficulty'
- explain how your measure depends on the angle of the bend and on the width of the road.
|
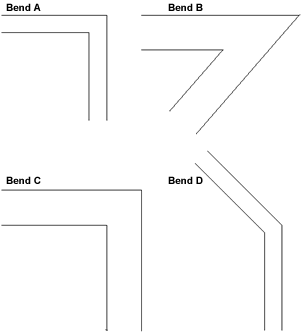
- To start with, imagine that you only travel parallel to the sides of a road.
So, ignoring the width of each road, put the four bends in order of "difficulty"
Explain your method clearly.
-
|
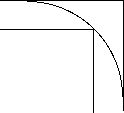
Now suppose you are able to cut corners along circular arcs.
Put the bends in order of "difficulty."
Explain how you do this. |
|
-
Find a way of measuring the 'difficulty' of a bend, taking into account that you can cut corners. Your measure should provide a single number for each bend which gives an indication of its 'difficulty'.
- Show how you can use your measure to place the four bends in order of difficulty. Compare what you get with your answer to question 2.
- Describe, in as much detail as you can, how your measure of difficulty depends on the angle of the bend and on the width of the road.
Square-ness, Example #1 (solution) || Steep-ness, Example #2 (solution)
Compact-ness, Example #3 (solution) || Crowded-ness, Example #4 (solution)
Awkward-ness, Example #5 (solution) || Sharp-ness, Example #6 (solution)

|

