
|
Tools - Math 'Creating Measures' Square-ness Task, Example #1
Square-ness, Example #1 (solution) || Steep-ness, Example #2 (solution)
Compact-ness, Example #3 (solution) || Crowded-ness, Example #4 (solution)
Awkward-ness, Example #5 (solution) || Sharp-ness, Example #6 (solution)
Malcolm Swan
Mathematics Education
University of Nottingham
Malcolm.Swan@nottingham.ac.uk
Jim Ridgway
School of Education
University of Durham
Jim.Ridgway@durham.ac.uk
This problem gives you the chance to:
- criticise a given measure for the concept of "square-ness"
- invent your own ways of measuring this concept
- examine the advantages and disadvantages of different methods.
|
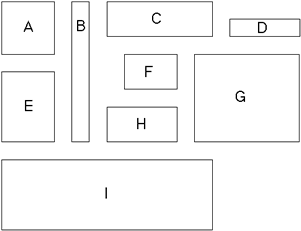
Warm-up
Use visual judgements to answer the warm-up questions.
Which rectangle looks the most square?
Which rectangle looks least square?
Without measuring anything, put the rectangles in order of "square-ness."
- Someone has suggested that a good measure of "square-ness" is to calculate the difference:
Longest side - shortest side
for each rectangle. Use this definition to put the rectangles in order of "square-ness."
Show all your work.
- Using your results, give one good reason why Longest side - shortest side is not a suitable measure for "square-ness."
- Invent a different way of measuring "square-ness." Describe your method carefully below:
- Place the rectangles in order of "square-ness" using your method. Show all your work.
- Do you think your measure is a good way of measuring "square-ness?" Explain your reasoning carefully.
- Find a different way of measuring "square-ness."
Compare the two methods you invented. Which is best? Why?
Square-ness, Example #1 (solution) || Steep-ness, Example #2 (solution)
Compact-ness, Example #3 (solution) || Crowded-ness, Example #4 (solution)
Awkward-ness, Example #5 (solution) || Sharp-ness, Example #6 (solution)

|

