Go to Collaborative Learning Go to FLAG Home Go to Search
Go to Learning Through Technology Go to Site Map
Go to Who We Are
Go to College Level One Home
Go to Introduction Go to Assessment Primer Go to Matching CATs to Goals Go to Classroom Assessment Techniques Go To Tools Go to Resources



Go to Tools overview
Go to Tool search
Go to Tools sorted by discipline
Go to Tools sorted by technique


Tools - Math 'Creating Measures' Sharp-ness Task, Example #6 (solution)


Square-ness, Example #1 (solution) || Steep-ness, Example #2 (solution)
Compact-ness, Example #3 (solution) || Crowded-ness, Example #4 (solution)
Awkward-ness, Example #5 (solution) || Sharp-ness, Example #6 (solution)

Malcolm Swan
Mathematics Education
University of Nottingham
Malcolm.Swan@nottingham.ac.uk

Jim Ridgway
School of Education
University of Durham
Jim.Ridgway@durham.ac.uk


This task gives you the chance to:
  • invent your own measure for the concept of 'difficulty' of going round a bend
  • use your measure to put bends in order of 'difficulty'
  • explain how your measure depends on the angle of the bend and on the width of the road.



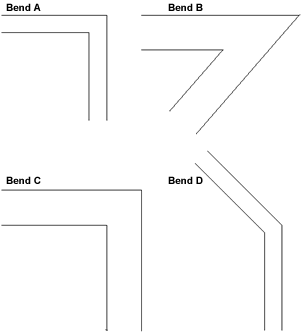
  1. To start with, imagine that you only travel parallel to the sides of a road.

    So, ignoring the width of each road, put the four bends in order of "difficulty"

    Explain your method clearly.



Solution:
Initially it makes sense to estimate the difficulty of a bend by the angle it turns through ( Greek letter theta ). Greater angles give greater difficulty:

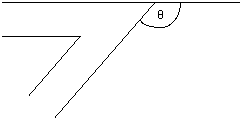
This gives 90o for bends A and C, 131o for bend B and 45o for bend D. Thus the order of difficulty of the bends is (from most to least difficult) B, A and C, D.







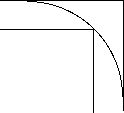
  1. Now suppose you are able to cut corners along circular arcs.

    Put the bends in order of "difficulty."

    Explain how you do this.



Solution:
At this stage, most students will probably try to answer the question by eye.

However, (anticipating question 4), if you try to draw the largest circular arc through each bend, you find that bends A and B will both allow arcs of radius 3.4 cm. Bend C will permit an arc of 6.8 (double the radius for bends A and B) and bend D will permit an arc of radius 13.1 cm.

Thus, the order of difficulty of the bends is now:

    A and B (tie for most difficult), C and D.







  1. Find a way of measuring the 'difficulty' of a bend, taking into account that you can cut corners. Your measure should provide a single number for each bend which gives an indication of its 'difficulty'.



Solution:
It may be seen that one possible measure for the 'difficulty' of a bend is radius of the largest circular arc that may be inscribed within the bend, that is tangential to the outer edges of the road.

The only drawback is that the larger this radius, r, the easier the bend. A measure which takes larger values for more difficult bends would be 1/r. This would take the'difficulty' value 0 for a straight road. The most difficult turn would be a U turn (when Greek letter theta = 180o). In this case r

Alternatively, one could define a measure using two variables, by reasoning in the following way:

  • If you keep the width constant, then the greater the angle of turn, the more difficult the bend is.
  • If you keep the angle constant, then the greater the width of the road, then the easier the bend is.

Thus we could define difficulty by a proportional model such as:







  1. Show how you can use your measure to place the four bends in order of difficulty. Compare what you get with your answer to question 2.



Solution:
See answer to question 2.







  1. Describe, in as much detail as you can, how your measure of difficulty depends on the angle of the bend and on the width of the road.


Solution:
Suppose the road is of width w, and turns through an angle Greek letter theta (which lies between 0o and 180o). We need to find the radius of the circular arc, r (r > w) which is tangential to the outside edges of the road and which just passes through the corner on the inside of the road (Q) in terms of w and Greek letter theta.



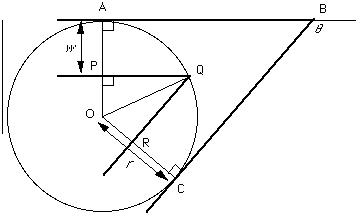
In triangle POQ:

    < OPQ is a right angle (the circle is tangential at A, and PQ is parallel to AB)

    OP = r - w

    OQ = r

    < POQ = Greek letter theta/2     (since OPQ is congruent to ORQ)


So, since OP = OQ cos (Greek letter theta/2)


This enables us to define the difficulty of any bend (1/r).

Notice that r is directly proportional to w. (This may also be seen, for example, by considering road C to be an enlargement of road A by scale factor 2, thus enlarging the radius by the same scale factor).

As Greek letter theta increases from 0 to 180o, cos (Greek letter theta/2) decreases from 1 to 0, so r decreases from an infinite radius to a radius of w.This corresponds to a U turn in a straight road width 2w.







Square-ness, Example #1 (solution) || Steep-ness, Example #2 (solution)
Compact-ness, Example #3 (solution) || Crowded-ness, Example #4 (solution)
Awkward-ness, Example #5 (solution) || Sharp-ness, Example #6 (solution)


Got to the top of the page.


Introduction || Assessment Primer || Matching Goals to CATs || CATs || Tools || Resources

Search || Who We Are || Site Map || Meet the CL-1 Team || WebMaster || Copyright || Download
College Level One (CL-1) Home || Collaborative Learning || FLAG || Learning Through Technology || NISE