
|
Tools - Math 'Creating Measures' Square-ness Task, Example #1 (solution)
Square-ness, Example #1 (solution) || Steep-ness, Example #2 (solution)
Compact-ness, Example #3 (solution) || Crowded-ness, Example #4 (solution)
Awkward-ness, Example #5 (solution) || Sharp-ness, Example #6 (solution)
Malcolm Swan
Mathematics Education
University of Nottingham
Malcolm.Swan@nottingham.ac.uk
Jim Ridgway
School of Education
University of Durham
Jim.Ridgway@durham.ac.uk
This problem gives you the chance to:
- criticise a given measure for the concept of "square-ness"
- invent your own ways of measuring this concept
- examine the advantages and disadvantages of different methods.
|
Warm-up
Use visual judgements to answer the warm-up questions.
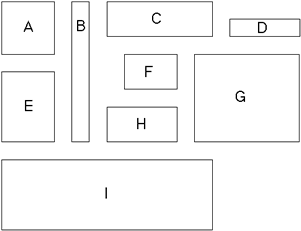
Which rectangle looks the most square?
Which rectangle looks least square?
Without measuring anything, put the rectangles in order of "square-ness."
Comment:
This first question is simply intended to orientate the students to the task in hand. It may be used as a class discussion.
- Someone has suggested that a good measure of "square-ness" is to calculate the difference:
Longest side - shortest side
for each rectangle. Use this definition to put the rectangles in order of "square-ness."
Show all your work.
Solution:
Using the measure 'Longest side - shortest side', the "square-ness" of each rectangle is given in the table below (using centimeters as the unit).
| Rectangle |
A |
B |
C |
D |
E |
F |
G |
H |
I |
| Dimensions (cm) |
3 x 3 |
1 x 8 |
6 x 2 |
4 x 1 |
3 x 4 |
3 x 2 |
6 x 5 |
4 x 2 |
12 x 4 |
| Square-ness (cm) |
0 |
7 |
4 |
3 |
1 |
1 |
1 |
2 |
8 |
Using this measure, the rectangles in order from most to least square are:
A, E and F and G (tie), H, D, C, B, I.
- Using your results, give one good reason why Longest side - shortest side is not a suitable measure for "square-ness."
Solution:
The above measure is unsatisfactory because:
- It gives no indication of the overall 'proportions'. (E, F and G under this definition have the same square-ness yet are clearly different in shape, while C and I are similar in shape but give different square-ness measures).
- It is dependent on the units used. If we use inches instead of centimetres we get a different "square-ness" measure.
- Invent a different way of measuring "square-ness." Describe your method carefully below:
Solution:
There are many other ways of measuring "square-ness." Students might, for example, propose using:
- The ratio longest side/shortest side;
- The largest angle between the diagonals of the rectangle;
- The ratio of perimeter/area.
a) and b) seem equally sensible. c), however, suffers the same problem as before. As it is not dimensionless, an enlargement of a rectangle will result in a different value for its "square-ness."
If, however, we use
- the ratio (perimeter)2 / area
then we would have a suitable, dimensionless measure.
- Place the rectangles in order of "square-ness" using your method. Show all your work.
Solution:
Whichever measure we now use (a), (b) or (d), we obtain the same order for the rectangles. In order of "square-ness" they are:
A (most square), G, E, F, H, C and I (tie), D, B (least square).
| Rectangle |
A |
B |
C |
D |
E |
F |
G |
H |
I |
| Dimensions (cm) |
3 x 3 |
1 x 8 |
6 x 2 |
4 x 1 |
3 x 4 |
3 x 2 |
6 x 5 |
4 x 2 |
12 x 4 |
Ratio:
longest ÷ shortest |
1 |
8 |
3 |
4 |
1.3 |
1.5 |
1.2 |
2 |
3 |
| Largest angle between diagonals |
90o |
166o |
143o |
152o |
106o |
113o |
100o |
127o |
143o |
Ratio:
Perimeter2 ÷ area |
16 |
40.5 |
21.3 |
25 |
16.3 |
16.7 |
16.1 |
18 |
21.3 |
- Do you think your measure is a good way of measuring "square-ness?" Explain your reasoning carefully.
Solution:
Here we would like students to review their results critically and decide whether the results from their measurements accord with their intuitions.
- Find a different way of measuring "square-ness."
Compare the two methods you invented. Which is best? Why?
Solution:
This question provides an opportunity for students to look for an alternative measure.
Square-ness, Example #1 (solution) || Steep-ness, Example #2 (solution)
Compact-ness, Example #3 (solution) || Crowded-ness, Example #4 (solution)
Awkward-ness, Example #5 (solution) || Sharp-ness, Example #6 (solution)

|

